1. 정보량
주머니에 N개의 서로다른 색의 공이 섞여있다고 가정하자. xi는 i번째 색의 공을 주머니에서 꺼내는 사건을 의미. xi의 확률이 높다면, 즉 너무 자주 발생하는 사건이라면 이로 부터 얻을 수 있는 정보는 적다. 반대로 xi의 확률이 낮다면, 즉 자주 발생하지 않은 사건이라면 이로 부터 얻을 수 있는 정보는 많다.

정보량은 위와 같이 표현한다.
2. 엔트로피 (Entropy)

x의 확률 분포 p(x)로 부터 기대되는 정보량. 엔트로피는 모든 사건이 동일한 확률을 가질 때 최대 값을 갖는다. 즉 p(x)가 Uniform Distribution 일 때 최대 정보량을 갖는다.
랜덤 변수 x, y의 joint distribution p(x,y)로 부터 기대되는 정보량은 joint entropy라 하며 다음과 같이 정의된다.

x, y가 서로 independent할 경우 다음이 성립된다.
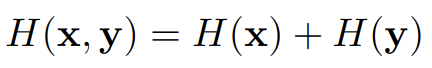
3. Mutual Information
Mutual Information의 정의는 아래와 같다.

x,y 각각으로 부터 기대되는 정보의 합에서 x,y를 동시에 고려했을 때 기대되는 정보의 차이이다. 즉 x와 y가 공통적으로 지니고 있는 정보의 양이라 볼 수 있겠다. 만일 x,y가 independent하다면 Mutual Information은 0이 되므로 x, y로 부터 공통적으로 기대되는 정보는 없다고 볼 수 있다.
4. Kullback-Leibler Divergence (KL Divergence)

x를 나타내는 두 분포 p와 q가 있다고 가정하자. KL-divergence는 아래와 같이 정의 된다.
가장 오른쪽 식의 첫번째 항 (-p x log q)는 x가 분포 q를 갖을때의 정보량을 두번째 항 (-p x log p)은 x가 분포 p를 가질 때의 정보량이다. KL-divergence는 항상 0보다 크거나 같으며 0인 경우 두 분포는 같은 정보를 갖는다.
쿨백-라이블러 발산은 어떠한 확률분포 P가 있을 때, 샘플링 과정에서 그 분포를 근사적으로 표현하는 확률분포 Q 를 P 대신 사용할 경우 엔트로피 변화를 의미한다. 따라서, 원래의 분포가 가지는 엔트로피 H(P)와 P 대신 Q를 사용할 때의 교차 엔트로피(cross entropy) H(P,Q)의 차이를 구하면 원래 정의했던 식과 같은 결과가 나온다.
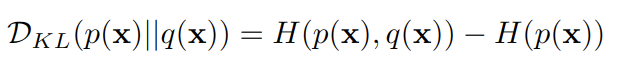
KL-Divergence는 다음과 같이 Mutual Information으로 표현이 가능하다.
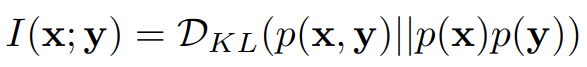
'Deep Learning' 카테고리의 다른 글
| Gaussian, LogGaussian PDF in Pytorch (0) | 2022.12.06 |
|---|---|
| Implement KL Divergence using Pytorch (0) | 2022.12.06 |
| Kullback–Leibler divergence (KL divergence) (0) | 2022.11.18 |
| Kullback–Leibler divergence (KL divergence) (0) | 2022.10.25 |
| How to make novel ideas? (0) | 2022.08.16 |

